GRAPHCNT 与 Dominator Tree

给你N个点M条边的有向图，问你无序二元组(X,Y)的个数，满足存在1->X与1->Y的路径，且不存在除了1以外的公共点。N<=100000

首先，要求出每个点到1上最先删去哪个点才能使它不与1联通。DAG可以搞搞每个点pre父亲，搞出一颗LCA树，但是不是DAG呢？

经邓司机指导，原来tarjan早在N年前已经解决了这个问题---Dominator Tree。可以参考LYD的讲稿。复杂度是O(N*a)的。

首先令T为一颗以r为根的有向有根树，即可以从r出发到达所有的点。

首先我们从r出发搞出一颗搜索树

idom(u)为u到根的最近必经点

semi(u)为u到根的最近半必经点。？？？就是在u的祖先中dfn[u]最小的点，且可以通过非树边不经过u到根上的其他的点到达u的点(好绕？)

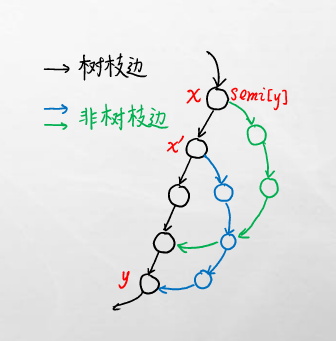
看看y是u点，那么x是他的semi，应为x可以先跳绿的边，在跳蓝的边，跳到y

注意如果一个点实在找不到semi了，他的直接树上父亲也可以作为他的semi

那肿么求呢？

首先我们看看，假设从u连入一些边，比如v->u，如果dfn[v]<dfn[u]，那么他是前向边(即从祖先过来的边)或树上的边，直接与semi取min即可

若dfn[v]>dfn[u]，那么是后向边或横叉边（？？脑补一下），那么v的一些最先的semi可以来更新答案。但不是所有的都可以，必须那些dfn比u大的点的semi可以来更新。为什么要dfn大于dfn[u]？因为如果小于的话，势必会经过u的祖先，于定义不符了。

具体求法：

先将点按dfn序大到小做

一开始将点的semi设为inf

然后枚举连向他的点，按照上面过程做。如何询问fn比u大的点的semi最小值？因为窝们从大往小做，所以dfn比大的都连在一块儿，用并查集维护即可。做完后将他和父亲连在一起即可

idom:

必经点定理：

一个点u的idom为：

u到semi[u]除了semi[u]以外路径上semi的最小值的那个点的idom值

具体做的时候可以在算semi是把每一个点挂到semi上，然后算出每个点的idom值是等于那个idom值，再顺推一遍即可

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <string>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <cmath>
#include <set>
#include <map>
using namespace std;
 
#define PII pair<int,int>
#define VPII vector<pair<int,int> >
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define sz(x) ((int)x.size())
#define rep(i,a,b) for (int i = a; i <= b; ++i)
#define dep(i,a,b) for (int i = a; i >= b; --i)
typedef long long ll;
ll power(ll x,ll y,ll mod){ll res=1;while (y){if (y&1) res=res*x%mod;x=x*x%mod;y>>=1;}return res;}
 
const int nn=100010;
 
int siz[nn],fa[nn],dfn[nn],id[nn],semi[nn],idom[nn],anc[nn],best[nn];
vector<int> suc[nn],pre[nn],dom[nn];
int n,m,ti;
void dfs(int x)
{
	dfn[x]=++ti;id[ti]=x;
	semi[ti]=ti;
	best[ti]=ti;
	anc[ti]=ti;
	rep(i,0,sz(suc[x])-1)
	{
		int y=suc[x][i];
		if (!dfn[y]) dfs(y),fa[dfn[y]]=dfn[x];
	}
}
int get(int x)
{
	if (x==anc[x]) return x;
	int y=get(anc[x]);
	if (semi[best[x]]>semi[best[anc[x]]])
		best[x]=best[anc[x]];
	anc[x]=y;
	return y; 	
}
void work()
{
	dep(y,ti,1)
	{
		int x=fa[y];
		rep(i,0,sz(pre[id[y]])-1)
		{
			int z=dfn[pre[id[y]][i]];
			if (!z) continue;
			get(z);
			semi[y]=min(semi[y],semi[best[z]]);
		}
		dom[semi[y]].pb(y);
		rep(i,0,sz(dom[x])-1)
		{
			int z=dom[x][i];
			get(z);
			if (semi[best[z]]<x) idom[z]=best[z];
			else idom[z]=x;
		}
		anc[y]=x;
	}
	rep(i,2,ti) if (semi[i]!=idom[i]) idom[i]=idom[idom[i]];
	idom[1]=0;
}
int main()
{
//	freopen("1.in", "r", stdin);
//	freopen("1.out", "w", stdout);
	scanf("%d%d",&n,&m);
	rep(i,1,m)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		suc[x].pb(y);
		pre[y].pb(x);
	}
	dfs(1);
	work();
	ll res=(ll)ti*(ti-1)/2;
	dep(i,ti,2)
	{
		int x=id[i];
		siz[x]++;
		int fx=id[idom[i]];
		siz[fx]+=siz[x];
		if (idom[i] == 1) res-=(ll)siz[x]*(siz[x]-1)/2;
	}
	cout << res << endl;
	return 0;
}