nblt's Blog

GRAPHCNT 与 Dominator Tree

给你N个点M条边的有向图，问你无序二元组(X,Y)的个数，满足存在1->X与1->Y的路径，且不存在除了1以外的公共点。N<=100000

首先，要求出每个点到1上最先删去哪个点才能使它不与1联通。DAG可以搞搞每个点pre父亲，搞出一颗LCA树，但是不是DAG呢？

经邓司机指导，原来tarjan早在N年前已经解决了这个问题---Dominator Tree。可以参考LYD的讲稿。复杂度是O(N*a)的。

首先令T为一颗以r为根的有向有根树，即可以从r出发到达所有的点。

首先我们从r出发搞出一颗搜索树

idom(u)为u到根的最近必经点

semi(u)为u到根的最近半必经点。？？？就是在u的祖先中dfn[u]最小的点，且可以通过非树边不经过u到根上的其他的点到达u的点(好绕？)

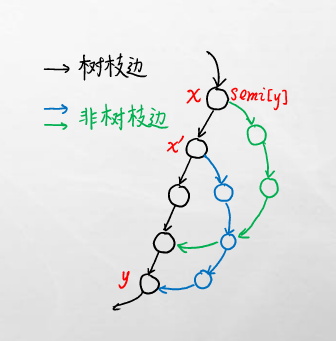
看看y是u点，那么x是他的semi，应为x可以先跳绿的边，在跳蓝的边，跳到y

注意如果一个点实在找不到semi了，他的直接树上父亲也可以作为他的semi

那肿么求呢？

首先我们看看，假设从u连入一些边，比如v->u，如果dfn[v]<dfn[u]，那么他是前向边(即从祖先过来的边)或树上的边，直接与semi取min即可

若dfn[v]>dfn[u]，那么是后向边或横叉边（？？脑补一下），那么v的一些最先的semi可以来更新答案。但不是所有的都可以，必须那些dfn比u大的点的semi可以来更新。为什么要dfn大于dfn[u]？因为如果小于的话，势必会经过u的祖先，于定义不符了。

具体求法：

先将点按dfn序大到小做

一开始将点的semi设为inf

然后枚举连向他的点，按照上面过程做。如何询问fn比u大的点的semi最小值？因为窝们从大往小做，所以dfn比大的都连在一块儿，用并查集维护即可。做完后将他和父亲连在一起即可

idom:

必经点定理：

一个点u的idom为：

u到semi[u]除了semi[u]以外路径上semi的最小值的那个点的idom值

具体做的时候可以在算semi是把每一个点挂到semi上，然后算出每个点的idom值是等于那个idom值，再顺推一遍即可

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <string>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <cmath>
#include <set>
#include <map>
using namespace std;
 
#define PII pair<int,int>
#define VPII vector<pair<int,int> >
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define sz(x) ((int)x.size())
#define rep(i,a,b) for (int i = a; i <= b; ++i)
#define dep(i,a,b) for (int i = a; i >= b; --i)
typedef long long ll;
ll power(ll x,ll y,ll mod){ll res=1;while (y){if (y&1) res=res*x%mod;x=x*x%mod;y>>=1;}return res;}
 
const int nn=100010;
 
int siz[nn],fa[nn],dfn[nn],id[nn],semi[nn],idom[nn],anc[nn],best[nn];
vector<int> suc[nn],pre[nn],dom[nn];
int n,m,ti;
void dfs(int x)
{
	dfn[x]=++ti;id[ti]=x;
	semi[ti]=ti;
	best[ti]=ti;
	anc[ti]=ti;
	rep(i,0,sz(suc[x])-1)
	{
		int y=suc[x][i];
		if (!dfn[y]) dfs(y),fa[dfn[y]]=dfn[x];
	}
}
int get(int x)
{
	if (x==anc[x]) return x;
	int y=get(anc[x]);
	if (semi[best[x]]>semi[best[anc[x]]])
		best[x]=best[anc[x]];
	anc[x]=y;
	return y; 	
}
void work()
{
	dep(y,ti,1)
	{
		int x=fa[y];
		rep(i,0,sz(pre[id[y]])-1)
		{
			int z=dfn[pre[id[y]][i]];
			if (!z) continue;
			get(z);
			semi[y]=min(semi[y],semi[best[z]]);
		}
		dom[semi[y]].pb(y);
		rep(i,0,sz(dom[x])-1)
		{
			int z=dom[x][i];
			get(z);
			if (semi[best[z]]<x) idom[z]=best[z];
			else idom[z]=x;
		}
		anc[y]=x;
	}
	rep(i,2,ti) if (semi[i]!=idom[i]) idom[i]=idom[idom[i]];
	idom[1]=0;
}
int main()
{
//	freopen("1.in", "r", stdin);
//	freopen("1.out", "w", stdout);
	scanf("%d%d",&n,&m);
	rep(i,1,m)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		suc[x].pb(y);
		pre[y].pb(x);
	}
	dfs(1);
	work();
	ll res=(ll)ti*(ti-1)/2;
	dep(i,ti,2)
	{
		int x=id[i];
		siz[x]++;
		int fx=id[idom[i]];
		siz[fx]+=siz[x];
		if (idom[i] == 1) res-=(ll)siz[x]*(siz[x]-1)/2;
	}
	cout << res << endl;
	return 0;
} 

第一次写与仙人掌有关的题目，虽然不是动态XXX

这个题目很有趣，问你有多少个同构的仙人掌

首先，仙人掌的问题肯定是要转换成树的问题的，那么可以先找出所以的环，对于每个环新建一个点，向所以这个环上的点连边，把环的边去掉，为了方便，在其他树边上新建一个中点，好，这样就转换成了树，并且等价。

现在考虑要找一个点它是不动的，显然是直径的中心，它不可能和其他的点换，而且新构的树中心是唯一的。把它拎起来，变成有根树。

剩下的考虑一个点，如果它不是环上的，那么如果有K个子树完全相同，那么有K！种方案。怎么判树相同？可以sort一下暴力hash，从小到大标号。

如果是环的中心，那么它不能随便交换，要考虑环上轮换（非中心不用考虑），或者对称，这个是字符串的基础问题了。

然后要考虑如果中心是环的中心，要考虑轮换

注意：

扫描环的时候要考虑顺序

偶环的对称有两种情况，都可以转换成回文串问题

由于最近越来越颓，为了增加动力，就写下来吧。。

(dp地狱训练）

SRM 503 DIV1    500pt ( 求期望题.贪心，枚举，概率计算 ) 答案分成两点之间的答案，再组合数统计即可。注意dist相同的情况，可以规定优先级。。先连city，再按顺序连village，这样就很方便了。。ll没开怎么死都不知道！！

SRM 507 DIV1    900pt ( dp+组合数学基础 ) 直接暴力dp即可

SRM 495 DIV1    975pt(数学， dp）一开始不会，可耻的去膜题解，然后发现了诡异的转移。。看了很久没看懂，YY了很久，终于在一个晚上想明白了。。我是个傻逼。。。题意是给你高度为H的楼房，让你用n个电梯覆盖，覆盖是这样的，保持电梯的相对位置不变，不遗漏的覆盖完，问方案数。如H=8,N=4 12123434。然后令f(H,N)表是前两个是不同的电梯覆盖，g(H,N)表示是相同的电梯覆盖，然后观察序列，发现1-N序列连续的块大小是定值，然后就f(H,N)就枚举块的大小,有f(H,N) = sigma g(H/d,N/d) (d>1, d|N) 现在考虑g(H,N)的转移,有g(H,N) = f)H,H/N) 可以这样理解，着相当于将所有的1由1-H/N替代，由于前两个都是1，这样的方案对应一个前两个是不同的电梯覆盖的方案。这样就可以了。:-D

TCO'10 Wildcard Round 500pt

题意：给你一堆带符号的卡片包含（+,-,*），随机抽取成排列，求期望表达式的值

注意到每一个非乘号后面均是等价的，所以分开来算，只要把所有非乘号的卡片的和加起来再乘上每一段的期望。而每一段的期望等价于开头全是乘号的期望积，枚举连续的K个，简单统计即可。很拙，思考了很久。

SRM 498 DIV1   1000pt

题意:求从(0,0)走到(Tx,Ty)且步长不超过(Mx,My)且有一些bad走法(dx=dy且为10倍数)问方案数

没想出来，看题解的。容斥走了几步坏的,注意到步子是可以交换的，然后dp再组合数统计没了。。感觉很厉害

TCO'10 Semifinal 1    950pt

一开始想残了，然后YY了很久才搞出来。。比较恶心的dp.枚举再前后dp一遍即可

SRM 522 DIV1   1050pt

题意：给你一些y[i]代表点(i,y[i])，每一次可以删除以两个点为对角线矩形内的点，问最终点剩余的可能方案

一开始没想法，其实这题是很好想的。首先我们观察最终留下的状态，那么显然是左右端点以及ymax与ymin的点，唯一有变化的是与左右y坐标相同的一些点，简单dp即可。

SRM 521 DIV1 500pt

题意：给你一些点，可以选择边长在lown到highn之间选择正方形去覆盖，问可能的集合数

显然不会太多，然后枚举左上与右下，简单判即可

SRM 481 DIV1   500pt

题意：给你一些人的任务，同一个人有多个任务。求安排任务顺序，使得平均等待时间最小。只有一台机器，且在最优方案中等概率选择，问每个任务完成的期望

每个人的任务总是连在一起的，简单计算即可。

SRM 521 DIV1   1000pt

题意：一个烟囱是由4个1*2的砖垒成一层，问你垒N层的方案数（只有下面的堆玩才能堆上面的）

一开始想不出状态定义，感觉很复杂，后来开了一下脑洞，只要考虑放第i层第一个后前两层的状态，只有4种情况，转移矩阵系数挺烦的，暴力状压算即可。

SRM 520 DIV1    500pt

sb背包

SRM 520 DIV1   1000pt

题意：给你一些哪些人cha过人以每个人被cha的转态，询问cha不同的序列数。每个人仅cha一次，而且被cha以后不会去cha别人。

非常神。一开始没有什么想法，去膜题解。好巧妙！当你搞不清关系时，可以列表，转换成形象的图形。而且显然可以将人分类。先放既cha人又被cha的，再放其他人。dp+组合排列

SRM 519 DIV1    600pt

ac自动机+dp

SRM 519 DIV1    900pt

枚举2,3相互搞的数量，再剩下与5,7匹配即可。注意怎么开数组（vector)

SRM 518 DIV1   500pt

貌似随便写了个贪心过了

SRM 518 DIV1   1000pt

本来是fwt的，但不会，学习了简单易懂的分治乘，而且复杂度是NlogN的。

SRM 517 DIV1    600pt

题意：操作i可以是a[i]与a[i+1]交换，给你一个目标排列，问你用1-i-1的i-1个操作排列使1--i-1变成目标排列，问排列方案数

很考思维，注意到操作i之前左右的数值不会交换，令f[i][j]为将i--j搞成有序的方案数，那么枚举最后一个操作，就变成了两个子问题。关键是要发现dp子问题的性质。

SRM 517 DIV1    900pt

题意：给你一个字符board，每次可以染一行或一列。问你最小次数

首先这种问题一般方法是先枚举一下，再推出一些信息。可以证明肯定有一行或一列不用染（反正，如果都染，那么第一次的会被全部覆盖),然后就知道了一行或一列的染色，再看不合法的点肯定让另一维染，搞出拓扑图判断。注意如果行列颜色都一样就没有限制关系！！

SRM 516 DIV1    500pt

简单的贪心

SRM 515 DIV1    550pt

题意：给你一些人到达店买剑的时间，价钱以及概率，每个人最多买一把剑，问你最多买K把剑的最优期望

可以dp[mask][i][j]表示mask的到过店，有i把剑，时间为t，dp即可。我觉的最难的是他告诉你每个时间到达店的概率，这样没法dp，而我们能做到的dp是用p[i]表示到以及(1-p[i])表示不到的概率进行转移，所以要把概率转一下，这点非常非常关键！！

SRM 515 DIV1   1000pt

题意：给你N*M的棋盘，有一些障碍点，三种人分别有他们的起始位置，各部相同，等概率出现在对应的位置上，三种人到达同一点，求走最短路的期望，两种人数<=20(N,M<=50)

一开始感觉很困难，两种人显然是要枚举的，但第三种人感觉很难再N*M的复杂的内求出。看了题解之后，忽然感觉很简单，N*M的复杂度只能BFS一遍，那么就考虑一种构图方法，使得求出的第三种人的距离为三个人最短路的答案，那么就很简单了，先枚举前两个人，再枚举三个人的聚集地点，然后对于每种前两个人到达聚集点的距离建一个点，距离i向距离i+1连边，然后每个距离向合法的到达点连边，再跑一遍BFS即可。很巧妙，关键是要想到可以直接BFS最终的距离和。

SRM648 DIV1 850pt

题意：求N个点K个桥带标号的图的个数

好难，首先图可以分成一个一个联通块背包do，然后一个联通块可以将桥拆掉变成若干个双联通分量，由矩阵树定理可得：N个带标号的点S个联通块(大小为mi)加S-1条边使图联通的方案数为N^(S-2)*pi(ai)。然后就算N个点的双联通分量有几个，可以先算出所有的联通图数量，再减去1-N-1座桥的图的数量。

SRM 510 DIV1    500pt

题意：仅有4,7构成的数是lucky number，A从[a,b]中选出连续的L1个，B从A选出的中选出连续的L2个。A要最大化lucky number的数量，B要最小化lucky number的数量，问最终结果(a,b<=10^10)

一开始很乱，感觉直接贪心边界十分不好处理，情况也非常多。然后去看了题解，看了将B从x选起的结果用F(X)表示出来，立马就懂了，可以发现函数值是连续的，就可以分成一些段搞了。然后枚举答案，看是否存在L1长度连续的即可。关键思路是将复杂的东西具体化，暴力化，用函数表示出来，就很显然了。

SRM 510 DIV1    1000pt

题意：仅有4,7构成的数是lucky number，给你N(N<=1e16)，问你有多少D是的ND进制下每一位是lucky number

首先方案不会太多，可以考虑枚举。但怎么枚呢？首先考虑假如有很多位那么D应很小，爆枚即可。当有2-3位时，看似很难枚，但由于数字只能是4,7构成，爆搜一下发现发难数都很少，check一下就可以了。关键是要先转化到位数很少的情况，再考虑爆枚。

SRM 658 DIV1    850pt

 二分图最大匹配，然后判一判即可

SRM 658 DIV1    650pt

题意：给你N个怪物(N<=20),每个怪的血值(<=60)，每次attck可以选择三个，分别扣血1,3,9滴，问你最少几次

首先可以二分答案，然后呢,发现如果选完3,9，剩下的只能选一到满，令dp[o][k][l]表示搞到第i个人3,9用了j,k个的最少1个数。dp即可。关键在于发现1取到满即可的性质

TCO Round3 2A 1000pt

题意：问你A^B有多少种不同的数，1<=A<=1e9, 1<=B<=1e9

首先可以将每个A^X表示成(r^k)^X,其中r为不能表示成更小的指数幂形式，那么可以知道k<=30，故暴力枚举k，先考虑如何统计最大次幂为k的r有几个，可以考虑容斥，答案等于sigma(i,mu[i]*这段区间中能表示成i次幂的数的个数)。

好，然后考虑对一个r不同的方案数，那么可以转换成k*X的方案数。这个怎么算呢，首先观察到k很小，考虑分段，对于(i*X,(i+1)*X]这段的答案，显然只有i+1到k乘才会合法，而对于i能覆盖所有i的倍数覆盖的点，那么考虑容斥，只要考虑哪些不构成倍数关系的数即可，这样最多只有15个左右，就可以了。关键是要想到优化容斥，直接容斥是2^30次，而分段则可以优化很多。

1的情况要特殊考虑。

TCO Round3 2A 600pt

题意：一个Magic Matrix定义为所有行和列的和的最后一位相同。每个格子只能填0-9.问你在N(<=1)个格子已填的基础上，有多少种不同的方案。

首先，如果N很大，那么可以将空的一行和一列交换到最后，这样可以直接算出！！

如果N很小，暴力搞死消元。关键是要想到可以交换的性质。

SRM578 DIV1 1000pt

题意：给你N个节点的树(N<=50),让你割掉一些边形成若干个联通子树，选出两棵子树，使它们同构。问最大点数

好难！首先可以考虑对于两棵有根树该怎么办，可以递归算出两个儿子分别匹配的答案，然后最优匹配即可。

然后可以枚举一条边删掉，然后枚举两个联通快的根，统计答案取max

关键是想到对于两棵有根树该怎么做。可以递归得到儿子答案，在最优匹配合并。/(ㄒoㄒ)/~~

SRM578 DIV1 500pt

题意长度为N(<=300)的线段上每个点可能有fox，现在给你一些条件，形如[L,R]这段区间至多有两个fox。问方案数

首先观察N的范围，考虑N^3的dp。令dp[i][j]表示i,j上有为相邻fox的方案数。这道题关键是用到最多两个的性质，直接上两维状态表示即可。O(∩_∩)O

TCO13 Semifinal1 550pt

题意：给你一个DAG的拓扑序列，一个DAG序列生成的方式是等概率随机当前入度为0的集合中的一个点加到序列。问你这个DAG中有A->B这条边的概率是多少

可以从后往前dp，设dp[i][j]表示到第i个点，后面的点是不是入度为0(用j表示一个二进制)的概率。直接算即可。最后必须有这条边的概率与所有概率除一除即可 O(∩_∩)O

SRM 509 DIV1 1000pt

题意：给你一个凸多边形，以及内部的N个点，每个点分配周长的1/N，问你内部的点到分配的点的最大值的最小值是多少？

二分，然后怎么判，先枚举每条线段，与每个圆作交，求出每个交点，在对每一段建点，跑网络流看是否满流即可。判线段与圆的交，设交点为X+w*d，d为直线向量，这样比较方便。注意eps。关键是讲复杂的交法转换成每一条边与每一个圆的交，算计技巧以很重要。/(ㄒoㄒ)/~~

SRM 507 DIV1    500pt

题意：给你Ns个1*1*1的方块和Nb个L*L*L个方块，用体积最小的长方体装下这些方块，求最小体积(要求平行）

一开始不会做，后来抱着试试看的心态，写了L*L*x，发现过了4个点，然后就发现答案最大值最多加L*L-1，然后写了个爆枚体积，分解因数判断的。。

后来看了题解，发现傻逼了。。由于题目中给出体积小于int，故直接枚举最短边，次短边在算第三条边即可。。关键是想到题解很小，而且爆枚两个最小边的复杂度很小。。。^_^

这题很早就碰到了，感觉很神，做法很怪异，题解看不懂。今年丽洁WC又讲了，终于下定决心把它搞掉。。

今天在去领会了一下，其实想法也挺自然的。。

首先，分成两类边：

1.只有数字相同，color不同

2.color同，数字不做要求

可以想象，如果把2类边删去，一行将变成一块一块的，我们只关心每一块的头尾颜色，这样，可以转换为三种颜色三个点，之间有一些边，我们可以将一块压缩成一条边，这样暴力dp找一条路径经过所有的边

然后注意到每一块数字都是相同的，且数字相同，颜色相同的不超过三张，这意味着总共不超过9张，搜！开一个hash记录每种边数量的状态（9种边），然后再开个数组像背包一样每种数字转移过来。。

这样就算出每种状态的数量，再乘上该状态下欧拉路径的数量加起来即可。

复杂度 最终转换的图状态只有几百w左右，跑得出来很，没有理论上的那么多

今天终于将那道令人发指的题做掉了。。

题意是給定一棵树，在线询问编号L--R中距离点X最近的点是多少

首先，如果L--R固定，哪么我们检出L--R的虚树，然后询问。。那么对于L--R我们只要按1--N区间建立区间虚树，线段树查寻即可。。

问题看似解决了？？？但总感觉线结很多。。

首先怎么存区间的虚树？ 我们可以对点开 vector 记录虚树dfs序即可。。。。怎么快速的在虚树上查寻？我一开始觉得很麻烦。。那些不是范围内的点怎么办？其实我们可以计算出每个不在范围内的点到在范围内的点的最短距离，这样就等价于在范围内的点了（有点想 codechef 的 BTREE）。然后怎么在dfs序中查寻距离最短的点？我们将每个点出与入记录到dfs序中，这样lower_bound待求点的dfs序号。。这样在左边的点与右边的点取min。。还有左边点的father（即自己的father）也可能成为答案。。这样就好了。。还有一种情况，就是待求点dfs序是max， 那么与虚树根节点求min即可。。

最后还被卡常数。。。时限3s 我跑了3s+。。怒开大时限。那么总的复杂度是 Nlog^2N

最近感觉有点虚。。所以重回这个blog写点东西。。

稳稳的完挂了。。

没什么可后悔的，自己太弱了，这是事实。。

还得努力刷题。。

祝愿进队的大爷么NOI顺利夺Au，怒艹IOI。。

  这几天一天不如一天，rating做一场跌一场，该写写回忆录。。

[CQOI]

  被和谐矩阵一题ken

5月16日  

  今天考HNOIday2，第一题，只会N方枚举，然后O(n)验证，我写着写着，发现要写KMP和AC自动机，直接放弃了写暴力了。。第二题暴力。第三题，一开始SG没想清楚，脑补了一下取石子游戏，然后有重写了一个。结果还是biubiu了。后来发现清0是j达成i了，然后写了70分暴力。然后发现有很多状态时多余的，只需sqrt(n)枚举即可。写完后，我FC，一开始以为对了，暴了几发OJ，wrong了，后来定睛一看，是“找不到文件”，而非“找不到差异”，顿时囧了。。暴力被删了，只得重写了一个，然后，然后稳稳的滚粗了。。biubiu！

5月17日

  今天SHTSC2014day1彻底萎穿了,为什么大家这么强？为是么我这么弱？第一题大意是求最小椭圆覆盖，我不会椭圆，觉得完全不可做，暴力都写不出！ 后来ZCC A了，告诉我不用椭圆的知识。我顿时有了信心，仔细思考了一下，只要将坐标压缩一下，求最小圆覆盖！！顿时成了逗比题，但是，我却只有50分。NMB!!经过调式，发现第一是精度挂了，后来被0除了。第二，是我随机增量时姿势不对，然后_Shi教我random_shuffle,数国又教我正确的姿势，蒟蒻长见识了！！第二题感觉不可作，第三题发现数是一列一列循环的，对于a<=1000的点，至多只有1000列，每一列中单增，只需暴力求列与列直接的逆序队，期望得分80，实际得分70。

  虽然今天垫底了，但我还是感觉收获不少。。